Question

The area of a square is given by x2, where x is the length of one side. Mary's original garden was in the shape of a square. She has decided to double the area of her garden. Write an expression that represents the area of Mary's new garden. Evaluate the expression if the side length of Mary's origanal garden was 8 feet

Answer 1

128 feet

Explanation:

N/A

Answer 2

`128\text{ ft}^(2)`

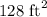
Explanation:

We have been given that the area of a square is given by
`x^2`, where x is the length of one side.

Mary's original garden was in the shape of a square. She has decided to double the area of her garden. So the new area of Mary's garden will be 2 times the area of original garden.

We can represent this information in an equation as:

`\text{Area of Mary's new garden}=2x^(2)`

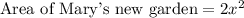
Therefore, the expression
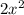`2x^2` will represent the area of Mary's new garden.

To evaluate the area of new garden, if the side length of Mary's original garden was 8 feet, we will substitute x equals 8 in our expression.

`\text{Area of Mary's new garden}=2(8\text{ ft})^(2)`

`\text{Area of Mary's new garden}=2*64\text{ ft}^(2)`

`\text{Area of Mary's new garden}=128\text{ ft}^(2)`

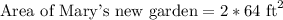
Therefore, the area of Mary's new garden will be 128 square feet.