Answer:
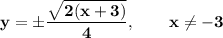
Explanation:
y = 8x² - 3 (Restriction: none - x is All Real Numbers)
The inverse is when you swap the x's and y's and then solve for y
x = 8y² - 3 swapped the x and y
x + 3 = 8y² added 3 to both sides
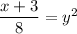 divided both sides by 8
divided both sides by 8
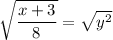 square rooted both sides
square rooted both sides
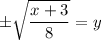 simplified
simplified
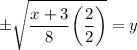 rationalized the denominator
rationalized the denominator
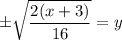 simplified
simplified
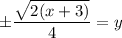 simplified
simplified
Restriction:
The radical (inside the square root sign) cannot be negative
→ 2(x + 3) ≥ 0
x + 3 ≥ 0 divided both sides by 2
x ≥ -3 subtracted 3 from both sides