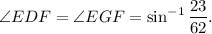Question

EASY TRIG - 15 POINTS

a . suppose the measure of one side of a triangle inscribed in a circle is 20 centimeters. If the measure of the angle in the triangle opposite this side is 30 degrees, what is the length of the diameter of the circle?
b. suppose a circle with a diameter of 12.4 inches circumscribes a triangle with one side of the triangle measuring 4.6 inches. What is the measure of the angle in the triangle opposite this side?

Answer 1

Answer: The answers are (a) 40 cm and (b)
`\sin^(-1)(23)/(62).`

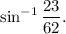
Step-by-step explanation: The calculations are as follows:

(a) See the figure (a). As given in the question, A circle with centre 'O' circumscribes a triangle ABC with BC = 20 cm and ∠BAC = 30°. We need to find the diameter DC of the circle.

Let us draw BD. Now, ∠BAC and ∠BDC are angles on the same arc BC, so we have

∠BAC = ∠BDC = 30°.

Also, ∠CBD = 90°, since it stands on the diameter DC. So, ΔBCD will be a right angled triangle.

We can write

`\sin \angle BDC=(BC)/(DC)\\\\\\ \Rightarrow \sin 30^\circ=(20)/(DC)\\\\\\\Rightarrow (1)/(2)=(20)/(DC)\\\\\\\Rightarrow DC=40.`

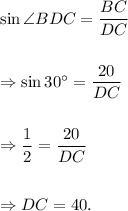
Thus, the diameter of the circle = 40 cm.

(b) See the figure (b).

As given in the question, A circle with centre 'O'' circumscribes a triangle DEF with EF = 4.6 inches and diameter GF = 12.4 in.. We need to find the angle EDF.

Let us draw GE. Now, ∠EGF and ∠EDF are angles on the same arc EF, so we have

∠EGF = ∠EDF = ?

Also, ∠GEF = 90°, since it stands on the diameter GF. So, ΔGEF will be a right angled triangle.

We can write

`\sin \angle EGF=(EF)/(GF)\\\\\\ \Rightarrow \sin \angle EGF=(4.6)/(12.4)\\\\\\\Rightarrow \sin \angle EGF=(23)/(62)\\\\\\\Rightarrow \angle EGF=\sin^(-1)(23)/(62).`

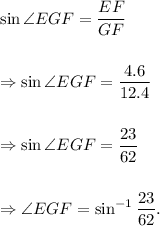
Thus,

`\angle EDF=\angle EGF=\sin^(-1)(23)/(62).`