Answer:
Steps explained below.
Explanation:
It is given that the vertices of the quadrilateral are G(1, -1), H(5, 1), I(4, 3) and J(0, 1).
A parallelogram is a rectangle if one of its angle is 90° (and therefore, all angles will be 90°).
A quadrilateral is a parallelogram if two pairs of opposite sides are equal.
So, lets prove GH = IJ, HI = GJ and H = 90°.
![GH^(2) =[1-(-1)\^]{2} +(5-1)^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/10mwodunoia5ohurg6hpv05bocfhds6t90.png)
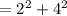
= 20
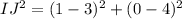
= 20
Therefore, GH = IJ


= 5
![GJ^(2) =[1-(-1)]^(2) +(0-1)^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/h4djp2a2h60h6dyi09ysju8tpx6rs1ozr2.png)

= 5
Therefore, HI = GJ
Two pairs of opposite sides are equal and hence GHIJ is a parallelogram.
Now, in Δ GHI,
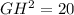
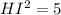
![GI^(2) =[3-(-1)]^(2) +(4-1)^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/43glbya8n52ny9vd622uktp47lxb5b65rj.png)
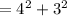
= 25
Therefore,
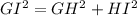 .
.
This shows that Δ GHI is a right angled triangle and ∠ H = 90°.
Hence, GHIJ is a rectangle.