Answer:
Option (c) is correct.
The solution of equation is b = 0 and b = 4.
Explanation:
The given equation,
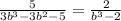
We are required to solve the given equation for possible values of b.
Consider,
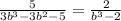
Cross multiply ,
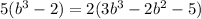
Multiply each term of LHS by 5 and RHS by 2 , we get,
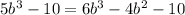
Taking variable terms one sides and constant one side, we get,
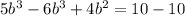
Solving , we get,
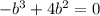
Taking
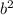 common from both terms, we get,
common from both terms, we get,
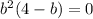
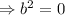 and
and
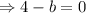
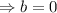 and
and

Thus, Option (c) is correct.
The solution of equation is b = 0 and b = 4.