Answer:
The length of the longest side are all real numbers greater than 39 inches and less than 51 inches
Explanation:
we know that
In an obtuse triangle
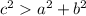
where
c is the length of the longest side
a and b are the two shorter sides
Convert the dimensions in inches
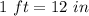
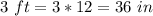
substitute the values
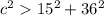
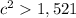
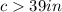
Applying the triangle inequality Theorem
1)
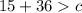
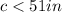
2)
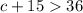
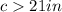
therefore
The length of the longest side belong to the interval
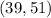
All real numbers greater than 39 inches and less than 51 inches