Answer:
A.

Explanation:
We have, the dimensions of the living room are 30 ft and 20 ft.
Thus, area of the living room = length × width = 30 × 20 = 600 ft².
Now, it is given that the cabinet takes 6% of the living room i.e. 6% of 600 ft² = 0.06 × 600 = 36 ft².
As, the triangle has dimensions (2x+3) ft and (3x+6) ft.
So, the area of the triangle =
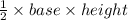
i.e. Area of cabinet =
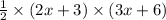
i.e. Area of cabinet =
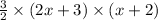
i.e. Area of cabinet =
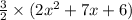
Since, the cabinet takes 6% of the living room, we have,
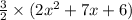 = 36
= 36
i.e.
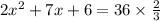
i.e.
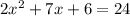
i.e.
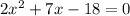
Further, as the solution of a quadratic equation
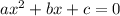 is given by
is given by
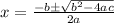
On comparing we have, a=2, b=7, c= -18.
Thus,

i.e.
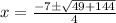
i.e.

i.e.
 and
and
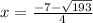
So, according to the options, we have,
A.
 is the correct value of x.
is the correct value of x.