Answer:
Thus, the two root of the given quadratic equation
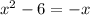 is 2 and -3 .
is 2 and -3 .
Explanation:
Consider, the given Quadratic equation,
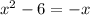
This can be written as ,
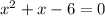
We have to solve using quadratic formula,
For a given quadratic equation
 we can find roots using,
we can find roots using,
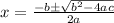 ...........(1)
...........(1)
Where,
 is the discriminant.
is the discriminant.
Here, a = 1 , b = 1 , c = -6
Substitute in (1) , we get,
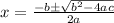
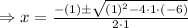
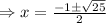
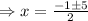
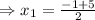 and
and
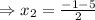
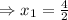 and
and
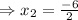
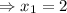 and
and
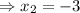
Thus, the two root of the given quadratic equation
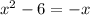 is 2 and -3 .
is 2 and -3 .