Question

Julius has a garden that has dimensions of 12 ft by 20 ft. Julius needs more room to plant some peppers, and determines the garden will need a new area of 360 square feet. How much should he increase the length and width by, if he wants to increase them by the same amount? Round your answer to the nearest tenth.

Answer 1

C. 3.4 feet

Explanation:

Let, the amount of increase be 'x' feet.

As, the length and width of the garden are 20 ft and 12 ft respectively.

It is given that the area of the new garden is 360 ft²

Since, the length and width are increased by 'x'.

The new length and width are (x+20) ft and (x+12) ft respectively.

So, we get,

New area,
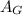`A_(G)` = length × breadth = (x+20) × (x+12)

i.e. 360 =
`x^(2)+32x+240`

i.e.
`x^(2)+32x-120=0`

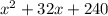
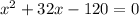
i.e. (x+35.4)(x-3.4)=0

i.e. x = -35.4 and x= 3.4

Since, the value of x cannot be negative.

Thus, x = 3.4 feet.