Answer:
B. 1.4 feet
Explanation:
Let, the amount of increase be 'x' ft.
Since, the length and width of the canvas are 4 ft and 3 ft respectively.
Thus, area of the canvas,
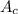 = length × breadth = 4 × 3 = 12 ft²
= length × breadth = 4 × 3 = 12 ft²
Since, the area of display model is twice the area of the canvas. We have,
 = 2 ×
= 2 ×
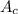
i.e.
 = 2 × 12
= 2 × 12
i.e.
 = 24 ft².
= 24 ft².
As, the length and width of the canvas are increased by 'x'.
The, length and width of the display model are (x+4) ft and (x+3) ft.
So, we get,
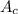 = length × breadth = (x+4) × (x+3) =
= length × breadth = (x+4) × (x+3) =

Since,
 = 24 ft²
= 24 ft²
i.e.
 = 24
= 24
i.e.
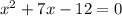
Solving the quadratic equation, we get,
i.e. x = -8.4 and x= 1.4
Since, the value of x cannot be negative.
Thus, x = 1.4 feet.