Answer:
Thus, the two root of the given quadratic equation
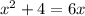 is 5.24 and 0.76 .
is 5.24 and 0.76 .
Explanation:
Consider, the given Quadratic equation,
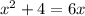
This can be written as ,
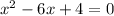
We have to solve using quadratic formula,
For a given quadratic equation
 we can find roots using,
we can find roots using,
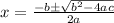 ...........(1)
...........(1)
Where,
 is the discriminant.
is the discriminant.
Here, a = 1 , b = -6 , c = 4
Substitute in (1) , we get,
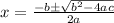
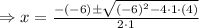
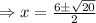
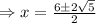
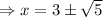
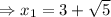 and
and

We know
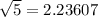 (approx)
(approx)
Substitute, we get,
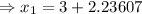 (approx) and
(approx) and
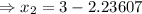 (approx)
(approx)
 (approx) and
(approx) and
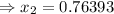 (approx)
(approx)
Thus, the two root of the given quadratic equation
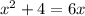 is 5.24 and 0.76 .
is 5.24 and 0.76 .