Question

A ball is thrown directly up in the air from a height of 5 feet with an initial velocity of 60 ft/s. Ignoring air resistance, how long until the ball hits the ground? Use the formula where h is the height of the ball in feet and t is the time in seconds since it is thrown. Round your answer to the nearest tenth.

Answer 1

3.8 seconds

Explanation:

Given equation

`h= -16t^2 + 60t + 5`

When the ball hits the ground then height is 0

So we replace h with 0 and solve for t

`0= -16t^2 + 60t + 5`

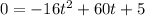
a= -16 , b= 60 and c= 5

Apply quadratic formula to solve for t

`t=(-b\pm √(b^2-4ac))/(2a)`

=
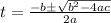
`(-60+√(60^2-4\left(-16\right)\cdot \:5))/(2\left(-16\right))[/tex</p><p>[tex]=(-60+-√(3920))/(-32)`

`=(-60+-28√(5))/(-32)`

`=(4(-15+-7√(5)))/(-32)`

`=((-15+-7√(5)))/(-8)`

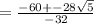
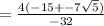
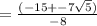
Now make two fractions and solve for x

t=
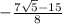`-(7√(5)-15)/(8)`=-0.0815

t=
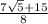`(7√(5)+15)/(8)`=3.83

So answer is 3.8 seconds