According to the Fundamental Theorem of Algebra, the graph of f(x) = x2 - 4x + 3, has roots. From the graph we can see that it has zeros.

Question

asked Oct 2, 2020 15.7k views

2 Answers

Anyname Donotcare · Answer 1 · 2020-10-07T15:31:48+0000

Answer:

The graph
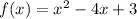has two zeros namely 3 and 1.

Explanation:

Consider the given equation of graph
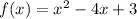
f(x)=x^2-4x+3

According to the Fundamental Theorem of Algebra

For a given polynomial of degree n can have a maximum of n roots.

Thus, for the given equation
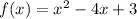f(x)=x^2-4x+3 the degree of polynomial is 2 , thus the function can have maximum of 2 roots.

We know at roots the value of function is 0 that is f(x) = 0,

Substitute f(x) = 0 , we get,
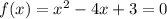
f(x)=x^2-4x+3=0

This is a quadratic equation,
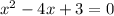
x^2-4x+3=0

We first solve it manually and then check by plotting graph.

Quadratic equation can be solved using middle term splitting method,

here, -4x can be written as -x-3x,

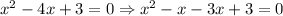
$x^2-4x+3=0 \Rightarrow x^2-x-3x+3=0$

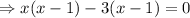
$\Rightarrow x(x-1)-3(x-1)=0$

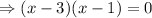
$\Rightarrow (x-3)(x-1)=0$

Using zero product property,
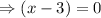$a\cdot b=0 \Rightarrow a=0\ or \ b=0$

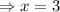$\Rightarrow (x-3)=0$ or
$\Rightarrow (x-1)=0$

$\Rightarrow x=3$ or
$\Rightarrow x=1$

Thus, the two zero of f(x) are 3 and 1.

We can also see on graph attached below that the graph
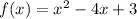has two zeros namely 3 and 1.