Answer:
Let x represents the number of lilies and y represents the number of tulips in the bouquet.
As per the statement:
A bouquet of lilies and tulips has 12 flowers.
⇒x+y = 12 .....[1]
It is also given that lilies cost $3 each and tulips cost $2 each the bouquet cost $32.
⇒
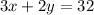 .....[2]
.....[2]
Multiply equation [1] by 3 we get;
3x+ 3y = 36 .....[3]
Subtract equation [2] from [3] we get;
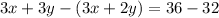
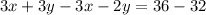
Combine like terms;
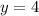
Substitute the value of y in [1] we get;
x + 4 = 12
Subtract 4 from both sides we get;
x = 8
Therefore, the number of lilies are 8 and the number of tulips are 4