Answer:
0
Explanation:
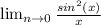
When we plug in 0 we will get 0/0
so we apply L' Hopitals rule
We take derivative at the top and bottom
derivative of sin^2(x) is 2sin(x)* cos(x)
2sin(x)cos(x) is sin(2x)
Derivative of x is 1
so limit becomes
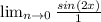
Plug in 0 for x to find limit
sin(2*0) = 0
So limit value is 0