Question

How many triangles in the diagram can be mapped to one another by similarity transformation?

Answer 1

Answer: the answer is 3

Explanation:

Answer 2

Answer: ΔABC, ΔDEF and ΔGHI are similar to one another.

Step-by-step explanation: We are given four triangles on the coordinate plane and we to check which can be mapped to one another by similarity transformation.

We have

In ΔABC, AC = 12 units, BC = AB = 6√2 units.

In ΔDEF, DF = 8 units, DE = EF = 4√2 units.

In ΔPQR, PR = 14 units, PQ = 10 units, QR = 6√2 units.

In ΔGHI, GH = 32 units, GI = IH = 16√2 units.

We can see that triangles ABC, DEF and GHI are isosceles but ΔPQR is not isosceles, so it cannot be similar to the others.

Also,

`(AB)/(DE)=(BC)/(EF)=(CA)/(DF)=(3)/(2),`

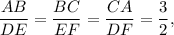
and

`(AB)/(IH)=(BC)/(GI)=(CA)/(GH)=(3)/(8),`

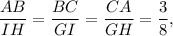
Therefore, ΔABC similar to ΔDEF and ΔABC similar to ΔGHI.

Therefore, ΔABC, ΔDEF and ΔGHI are similar to one another.