Question

For a circle with the radius of 15 cm what is the length of an ark intercepted by angle measuring 120?

Answer 1

Hello from MrBillDoesMath!

Answer:

10 Pi

Discussion:

Circumference of full circle = 2 Pi r = 2 Pi (15) = 30 Pi. As a circle contains 360 degrees, 120 degrees is one third of the circle and subtends an arc of

(30 Pi)/3 = 10 Pi

Thank you,

MrB

Answer 2

The length of an arc is, 31.41594 cm

Explanation:

The arc length of the circle(l) is given by:

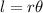`l =r \theta` ....1[]

where

r is the radius of the circle

`\theta` is the angle in radian.

As per the statement:

For a circle with the radius of 15 cm and angle is 120 degree.

⇒r = 15 cm and angle in degree = 120

Use conversion:

1 degree = 0.0174533 radian

then;

120 degree = 2.094396 radian

⇒
`\theta = 2.094396`

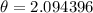
Substitute the given values in [1] we have;

`l = 15 \cdot 2.094396 = 31.41594`

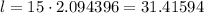
⇒l = 31.41594 cm

Therefore, the length of an arc is, 31.41594 cm