Question

The three lines 8x+3y=12, 6y-7x=24, x+9y+33=0 intersect to form a triangle. Find the coordinates of its centroid

Answer 1

coordinates of its centroid=(-1,-1)

Explanation:

The given three lines are:

8x+3y=12, (1)

6y-7x=24 (2)

and x+9y+33. (3)

Multiplying equation (1) by 2 and subtract the equation (2), we get

23x=0⇒x=0,

Putting the value of x=0 in equation (2), we get

6y=24

y=4

Now, multiply the first equation by 3 and subtract the equation (3), we get

23x=69⇒x=3

Putting the value of x=3 in equation (1), we get

24+3y=12

3y=-12

y=-4

Also, multiplying the equation (3) by 7 and add the equation (2), we get

69y=-207

y=-3

Putting the value of y=-3 in equation (2), we get

6(-3)-7x=24

-18-24=7x

x=-6

So the centroid is located at (the average of the three vertices):

`x=(0+3-6)/(3)=(-3)/(3)=-1` and
`y=(4-4-3)/(3)=(-3)/(3)=-1`.

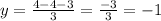Thus, the coordinates of its centroid=(-1,-1)