Question

Duffy was analyzing the trajectory made after throwing a football. his coach was able to measure that his throw reached a maximum height of 18 feet after 2 seconds. he figured that the ball left his hand at a height of 5 feet. Let the independent variable represent time and the dependant variable represent height of the ball. Use this information to write an equation to model the path of the ball and predict when the ball will hit the ground the ball will hit the ground at approximately ________ seconds

Answer 1

4.35 seconds.

Explanation:

Let x represent the time the independent variable and y be dependent variable (height of the ball).

We are told that Duffy figured that the ball left his hand at a height of 5 feet. This means at x equals 0, y was 5 or initial height of ball is 5 feet.

We have been given that Duffy's coach measured that his throw reached a maximum height of 18 feet after 2 seconds. This means that at x equals 2 y was 18.

As point (2,18) represents maximum height of ball, so it will be vertex of parabola.

Since initial height of ball is less than maximum height, so our parabola will be downward opening and leading coefficient will be negative.

We know that vertex form of a downward opening parabola is in form:
`y=-a(x-h)^2+k`

`y=-a(x-2)^2+18`

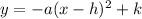
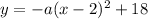
Let us find value of a using point (0,5).

`5=-a(0-2)^2+18`

`5=-a*4+18`

`5-18=-a*4+18-18`

`-13=-4a`

`(-13)/(-4)=(-4a)/(-4)`

`(13)/(4)=a`

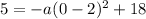
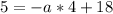
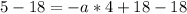
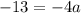
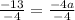
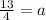
Therefore, the equation
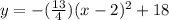`y=-((13)/(4))(x-2)^2+18` can be used to find the height of ball after x seconds.

To find the time it will take the ball to hit the ground, we will substitute y equals 0 in our equation.

`0=-((13)/(4))(x-2)^2+18`

`0-18=-((13)/(4))(x-2)^2+18-18`

`0-18=-((13)/(4))(x-2)^2`

`-18*((4)/(13))=-(x-2)^2`

`(72)/(13)=(x-2)^2`

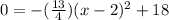
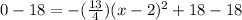
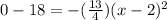
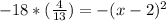
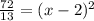
Taking square root of both sides of our equation we will get,

`\sqrt{(72)/(13)}=x-2`

`x-2\pm 2.35339`

`x-2=2.35339\text{ (or) } x-2=2.35339`

`x-2+2=2.35339+2\text{ (or) } x-2+2=-2.35339+2`

`x=4.35339\text{ (or) } x=-0.35339`

`x\approx 4.35\text{ (or) } x\approx -0.35`

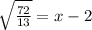
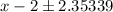
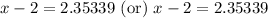
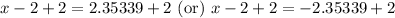
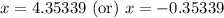
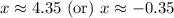
Since time can not be negative, therefore, the ball will hit the ground approximately after 4.35 seconds.