Question

Suppose DK is an angle bisector of △DEF.


Given: EK=2, FK=5, DF=10. Find DE.

Answer 1

`DE=4`

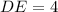
Explanation:

We have been provided a graph of a triangle and we are asked to find the length of segment DE.

Angle bisector theorem states that if a ray bisects an angle of a triangle, then it bisects the opposite side of triangle into segments that are proportional to other two sides.

By angle bisector theorem we can set proportions of the given sides as:

`(DE)/(EK)=(DF)/(FK)`

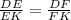
Upon substituting our given values in above proportion we will get,

`(DE)/(2)=(10)/(5)`

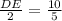
Upon multiplying both sides of our equation by 2 we will get,

`(DE)/(2)* 2=2* (10)/(5)`

`DE=2* 2`

`DE=4`

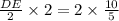
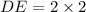
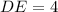
Therefore, the length of segment DE is 4 units.