Question

I need help with Multiplication Properties of Exponents desperately!! I've tried to solve both problems repeatedly and I cannot solve them. I really need to redo the assignment so any help is welcome!

P.S. My teacher said on the assignment that the first one is going to be a negative.

Answer 1

1) x= -36.

2) x = 0.

Explanation:

1) Taking the 3rd power to both sides and using the following exponent law:

`\left(a^b\right)^c = a^(bc)`

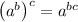
we get:

`\left(\left(m^(x)\right)^{(1)/(3)}\right)^3 = \left(m^(-12)\right)^3 \\ m^x = m^(-36)`

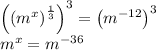
So this tells us that x = -36.

2) We can distribute the power inside every term. So the left side becomes:

`\left(3x^3y^x\right)^3 = 3^3\left(x^3)^3y^(3x) = 27x^9y^(3x)`

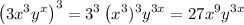
Now, the trick here is to remember that
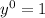`y^0 = 1`, so replacing 1 with
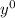`y^0`, which then gives us:

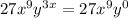`27x^9y^(3x) = 27x^9y^(0)`, telling us that 3x = 0 and thus, x = 0.