Question

Need help please show how you did it.

Answer 1

(0, 1).

Method 1 (Substitution):

Substituting our two y's, we get the following:

`x^2 + 5x + 1 = x^2 + 2x + 1 \Rightarrow 3x = 0 \Rightarrow x = 0`

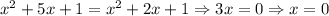
Thus, the only set of solutions is (0, 1). A quick sketch (either by hand or on Desmos) can confirm this.

Method 2 (Elimination):

We have two equations. We'll let the top one be equation 1 and the bottom one be equation 2. Eliminating as many variables as we can, we subtract (2) from (1) to get:

0 = 3x => x = 0.

So the only set of solutions is (0, 1).

Method 3 (Gaussian elimination):

We can place this in an augmented matrix and row reduce.

`\left[\begin{array}{cccc}1&5&1 & 1\\1&2&1 & 1\end{array}\right]`

Row reducing this gives us:

`\left[\begin{array}{cccc}1&5&1 & 1\\0&3&0 & 0\end{array}\right]`

This tells us that the only solution for x is x = 0 (since we read this as "3x = 0") and thus, the only solution we get is (0, 1).