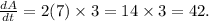Question

A square with side x is changing with time where x(t)=3t+1. What is rate of change of the area of the square when t=2 seconds.

Answer 1

Rate of change of the area of the square is 42 units at t = 2.

Explanation:

We note that the area of the square is given by:
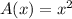`A(x) = x^2` but we aim to find
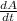`(dA)/(dt)`. But we can use the chain rule to pull out that dA/dt. Doing so gives us:

`(dA)/(dt) = (dA)/(dx) * (dx)/(dt).`

Now,
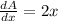`(dA)/(dx) = 2x` (by the power rule and
`(dx)/(dt) = 3.`

But since we have "x" and not "t", we want to find what x is when t = 2. Substituting t = 2 gives us x(2) = 3(2) + 1 = 7.

So, finally, we see that:

`(dA)/(dt) = 2(7) * 3 = 14 * 3 = 42.`