Answer:
It takes 7.5 seconds the object to hit the ground.
Explanation:
An object is propelled upward from the top of a 300 foot building. The path that the object takes as it falls to the ground can be modeled by:
h = -16t^2 + 80t + 300
where:
t is the time (in seconds) and
h is the corresponding height (in feet) of the object.
How long does it take the object to hit the ground?
When the objet hit the ground:
h=0
Then, equaling h (the equation) to zero:
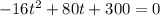
This is a quadratic equation. Using the quadratic formula:
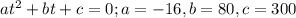

Two solutions:
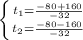
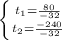
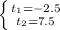
The first solution is not possible, because the time can't be a negative number, then the solution is the second one: t=7.5 seconds
Answer: It takes 7.5 seconds the object to hit the ground.