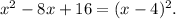Question

Evaluate the discriminant of the equation. Tell how many solutions each equation has and whether the solutions are real or imaginary.

x^2 = 8x - 16

Answer 1

x = 4

Explanation:

x^2 - 8x + 16 = 0

x^2 - 2 (x) (4) + 4^2 = 0

(x - 4)^2 = 0

x - 4 = 0

x = 4

Answer 2

One distinct and real solution.

Explanation:

Rearranging the equation gives us:

`x^2 - 8x + 16 = 0.`

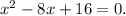
Using the discriminant, we get:

`\Delta = (-8)^2 - 4(1)(16) = 64 - 64 = 0.`

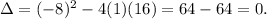
If the discriminant is 0, then we get only one distinct solution but really, we do have two roots (it's just the same magnitude). We say that the equation has only one solution.

And in fact, the equation can be factored as a perfect square:

`x^2 - 8x + 16 = (x - 4)^2.`