Question

Graph y = -­4x2 ­- 2 and its inverse.

Answer 1

Be careful with finding its inverse! An inverse only exists for one-to-one functions so we need to restrict the domain such that the quadratic is one-to-one. For brevity, we'll take the domain:
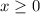`x \geq 0` but you could just as easily take
`x \leq 0`.

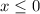Being that the quadratic is now one-to-one, we'll try to find its inverse.

By definition, an inverse function is the function flipped across the line y = x. So being that, we need to interchange the x and y coordinates around and then solve for y.

This gives us:

`x = -4y^2 - 2 \\ x + 2 = -4y^2 \\ -(1)/(4)\left(x + 2\right) = y^2 \\ y = \sqrt{-(1)/(4)\left(x + 2\right)}`

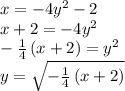
Now, this function is defined for when
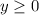`y \geq 0` and
`x \leq -2`.

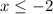So I'll end with this, what is the relationship between the domain/range of the original function and the domain/range of the inverse?