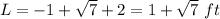Answer:
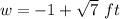
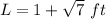
Explanation:
we know that
The area of a rectangle is equal to
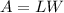
In this problem we have
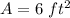
so
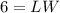 ------> equation A
------> equation A
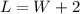 -----> equation B
-----> equation B
substitute equation B in equation A
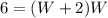
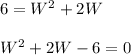
The formula to solve a quadratic equation of the form
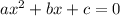 is equal to
is equal to
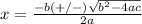
in this problem we have
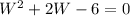
so
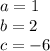
substitute in the formula
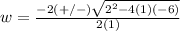
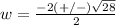
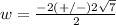
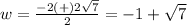 ------> the value positive is the solution
------> the value positive is the solution
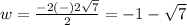
therefore
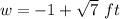
Find the value of L
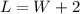 ------>
------>