Answer:
The length of line segment is 5
Explanation:
we are given equation of parabolas as

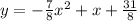
Firstly, we will find intersection points
we can set them equal
and then we can solve for x
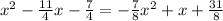
Multiply all sides by 8
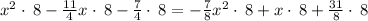
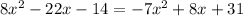

now, we can factor it
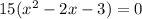
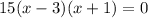
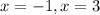
now, we can find y-values
At x=-1:
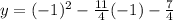
y=2
so, we get point as
(-1,2)
At x=3:
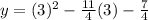
y=-1
so, we get point as
(3,-1)
now, we can find distance between these two points
(-1,2)
x1=-1 , y1=2
(3,-1)
x2=3 , y2=-1
now, we can find distance
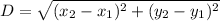
now, we can plug values

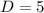
So,
The length of line segment is 5