Question

Given: △KOE∼△LSV, OT and SP are angle bisectors Prove: OT/TE = SP/PV

Answer 1

Explanation:

Since we have given that

Given: △KOE∼△LSV,

OT and SP are angle bisectors.

To Prove: OT/TE = SP/PV

Proof: Consider △OTE and △PSV,

∠E = ∠V (∵ △KOE∼△LSV)

∠KOE = ∠LSV

`(1)/(2)\angle KOE=(1)/(2)\angle LSV\\\\\angle TOE=\angle PSV`

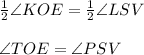
( ∵ OT and PS are the angle bisectors)

OE = SV (∵ △KOE∼△LSV)

By SAS criteria, △OTE ≈ △PSV

So, ratio will be

`(OT)/(TE)=(SP)/(PV)`

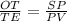
Hence, Proved.