I assume you don't know about derivatives yet. The reason I bring that up is because the given limit is equivalent to the derivative of a certain function and you might recognize it later on.
To compute the limit, in the numerator we can combine the fractions into one:
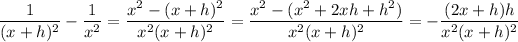
We're taking the limit as
 , which means we're considering
, which means we're considering
 near 0, but not
near 0, but not
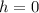 , so that we can simplify:
, so that we can simplify:
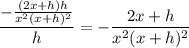
Then as
 , we have
, we have
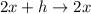 and
and
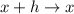 , so that
, so that
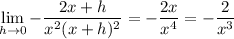
provided that
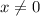 .
.
(In fact, the limit is equivalent to the derivative of the function
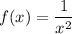 , whose derivative is
, whose derivative is
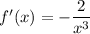 )
)