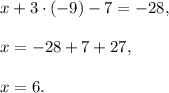Question

Solve the system of linear using gauss jordan elimination

2x +y -2z = -11

x +3y -z= -28

3x +4y -z= -25

Answer 1

x=6,

y=-9,

z=7

Explanation:

Rewrite the second equation in the first place

`\left\{\begin{array}{l}x+3y-z=-28\\2x+y-2z=-11\\3x+4y-z=-25\end{array}\right..`

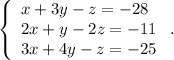
Multiply the first equation by 2 and subtract the second and then multiply the first equation by 3 and subtract the third:

`\left\{\begin{array}{l}x+3y-z=-28\\2x+6y-2z-(2x+y-2z)=-2\cdot 28-(-11)\\3x+9y-3z-(3x+4y-z)=-3\cdot 28-(-25)\end{array}\right.\Rightarrow \left\{\begin{array}{r}x+3y-z=-28\\5y=-45\\5y-2z=-59\end{array}.`

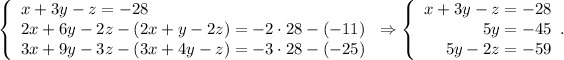
Write the variable y into the third column:

`\left\{\begin{array}{r}x-z+3y=-28\\-2z+5y=-59\\5y=-45\end{array}.`

From the last equation

`y=-(45)/(5)=-9.`

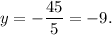
Substitute it into the previous equation:

`-2z+5\cdot (-9)=-59,\\ \\-2z=-59+45,\\ \\-2z=-14,\\ \\z=7.`

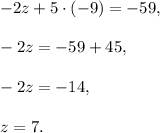
Substitute both y and z into the first equation:

`x+3\cdot (-9)-7=-28,\\ \\x=-28+7+27,\\ \\x=6.`