Answer:
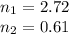
Explanation:
To solve this problem you must apply the proccedure shown below:
1. You have that the quadratic formula is:
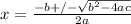
2. To solve the quadratic equation you must substitute the values. So, you have that:
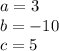
Then you have:
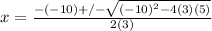
3. Therefore, you obtain the following result:
