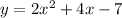1. Write a quadratic function, in standard form, that fits the set of points. Solve it as a system of three equations (-4, 9), (0, -7), and (1, -1)

Question

asked Feb 7, 2020 103k views

1 Answer

Mohamad Hamouday · Answer 1 · 2020-02-10T20:31:19+0000

Answer:

The equation is
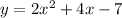
y=2x^2+4x-7

Explanation:

Let the quadratic function be

y=ax^2+bx+c

The point (-4,9) must satisfy this function,

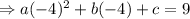
$\Rightarrow a(-4)^2+b(-4)+c=9$

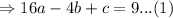
$\Rightarrow 16a-4b+c=9...(1)$

The point (0,-7) must also satisfy this function,

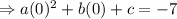
$\Rightarrow a(0)^2+b(0)+c=-7$

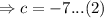
$\Rightarrow c=-7...(2)$

The point (1,-1) must also satisfy this function,

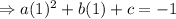
$\Rightarrow a(1)^2+b(1)+c=-1$

$\Rightarrow a+b+c=-1...(3)$

We put equation 2 into equation 1 to get;

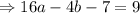
$\Rightarrow 16a-4b-7=9$

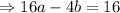
$\Rightarrow 16a-4b=16$

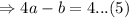
$\Rightarrow 4a-b=4...(5)$

We again put equation 2 into equation 3 to get;

$\Rightarrow a+b-7=-1$

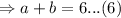
$\Rightarrow a+b=6...(6)$

We add equation 5 and 6 to get;

5a=10

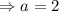
$\Rightarrow a=2$

We put
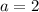a=2 into equation 6 to get;

2+b=6

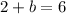
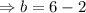
$\Rightarrow b=6-2$

$\Rightarrow b=4$

The equation is therefore
y=2x^2+4x-7