Question

A geometric sequence has an initial value of 1/2 and a common ratio of 8. Write an exponential function to represent this sequence.

A: f(X) = 8· (1/2)^x
B: f(X) = 8· (1/2)^-1
C: f(x) = 1/2 ·8^x
D: f(x) = 1/2 ·8^x-1

please help me

Answer 1

D

Explanation:

the n th term of a geometric sequence is

`a_(n)` = a
`r^(n-1)`

Where a is the first term and r the common ratio

here a =
`(1)/(2)` and r = 8, hence

f(x) =
`(1)/(2)`
`(8)^(x-1)` → D

Answer 2

The correct option is D.

Explanation:

It is given that the initial value of a GP is 1/2 and common ratio is 8. It means

`a_1=(1)/(2)`

`r=8`

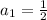
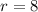
The nth term of a GP is

`a_n=a_1r^(n-1)`

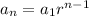
where,
`a_1` is inital value and r is common ratio.

Substitute
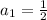`a_1=(1)/(2)` and
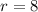`r=8` in the above formula.

`a_n=(1)/(2)(8)^(n-1)`

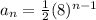
The exponential function to represent this sequence is

`f(x)=(1)/(2)(8)^(x-1)`

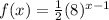
Therefore the correct option is D.