Answer:
As per the statement:
Hawick is 15 miles south of Abbotsford, and Kelso is 17 miles east of Abbotsford.
Let H represents Hawick , A represents Abbotsford and K represents Kelso
See the diagram as shown below:
Distance of AH = 15 miles
Distance of AK = 17 miles.
We have to find the distance HK:
Using Pythagoras theorem;
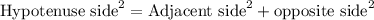
then;
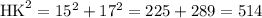
or
 miles.
miles.
Therefore, the distance from Hawick to Kelso( to the nearest tenth place) is 22.6 miles