Question

Can you help me with my homework

Answer 1

QUESTION 5a

The given function is
`f(x)=2x^2-32`

We factor to obtain;
`f(x)=2(x^2-16)`.

This implies that;

`f(x)=2(x^2-4^2)`.

We apply difference of two squares to obtain;

`f(x)=2(x-4)(x+4))`.

To find the solutions of the function, we solve
`f(x)=0`.

`2(x-4)(x+4)=0`

`(x-4)(x+4)=0`

`\Rightarrow (x-4)=0,(x+4)=0`.

`\Rightarrow x=4,x=-4`

The positive solution is 4

QUESTION 5b.

The given function is

`g(x)=12x^2-48`.

To find the solution, we solve
`g(x)=0`.

This implies that;

`12x^2-48=0`.

We divide through by 12 to get;

`x^2-4=0`

`x^2=4`

`x=\pm √(4)`

`x=\pm 2`

The positive solution is
`x=2`.

QUESTION 5c

The given function is
`h(x)=100x^2`.

To find the solution of this function, we solve the equation;

`100x^2=0`

This implies that;

`x^2=0`

`x=0`

Therefore the quadratic function with the biggest positive solution is ;

`f(x)=2x^2-32`.

QUESTION 6.

The height of the screwdriver is modeled by:

`h=-16t^2+98`

When the screwdriver reach the ground its height will be zero.

This implies that;

`-16t^2+98=0`

This implies that;

`-16t^2=-98`

We divide through by -16 to get;

`t^2=(-98)/(-16)`

`t^2=(49)/(8)`

`t=\pm \sqrt{(49)/(8)}`

`t=\pm (7)/(√(8) )`

`t=\pm 2.475`

Time is always positive, so we discard the negative value to get;

`t=2.5` seconds to the nearest tenth.

QUESTION 7

The given equation is

`x^2+c=103`

This implies that

`x^2=103-c`

`x=\pm √(103-c)`

`x=-√(103-c)`

or

`x=√(103-c)...eqn(1)`

We substitute
`x=9\:or-9` into either equation (1) or (2) to get

`9=√(103-c)...eqn(2)`

`9^2=103-c`

`81=103-c`

`81-103=-c`

`c=22`

We could have also substituted into

Answer 2

5. The quadratic function has a bigger positive solution is f(x)=2x^2-32.

6. It will take approximately 2.5 seconds for the screwdiver to reach the ground.

7. The value of c so that -9 and 9 are both solutions of x^2+c=103 is c=22.

Explanation:

5. f(x)=2x^2-32

Solution:

`f(x)=0\\ 2x^(2)-32=0`

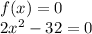
Solving for x: Adding 32 both sides of the equation:

`2x^(2) -32+32=0+32\\ 2x^(2) =32`

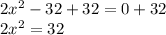
Dividing both sides of the equation by 2:

`(2x^(2) )/(2)=(32)/(2)\\ x^(2)=16`

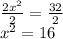
Square root both sides of the equation:

`\sqrt{x^(2) } =+-√(16)`

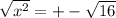
x=±4

Solution: x=-4 and x=4

g(x)=12x^2-48

Solution:

`g(x)=0\\ 12x^2-48=0`

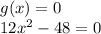
Solving for x: Adding 48 both sides of the equation:

`12x^(2)-48+48=0+48\\12x^(2) =48`

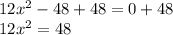
Dividing both sides of the equation by 12:

`(12x^(2) )/(12)=(48)/(12)\\x^(2) =4`

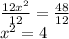
Square root both sides of the equation:

`\sqrt{x^(2) } =+-√(4)`

x=±2

Solution: x=-2 and x=2

h(x)=100x^2

Solution:

`h(x)=0\\ 100x^(2) =0`

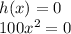
Solving for x: Dividing both sides of the equation by 100:

`(100x^(2) )/(100)=(0)/(100)\\ x^(2) =0`

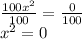
Square root both sides of the equation:

`\sqrt{x^(2) } =√(0)\\ x=0`

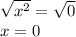
Solution: x=0

Answer: The quadratic function has a bigger positive solution is f(x)=2x^2-32.

6. h=-16t^2+98

How long will it take for the screwdiver to reach the ground?

In the ground h=0, then:

`-16t^2+98=0`

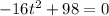
Solving for t: Subtracting 98 from both sides of the equation:

`-16t^2+98-98=0-98\\ -16t^2=-98`

Dividing both sides of the equation by -16:

`(-16t^2)/(-16)=(-98)/(-16)\\t^2=6.125`

Square root both sides of the equation, taking only the positive value, because the time must be a positive number:

`√(t^2)=√(6.125)\\t=2.474873734`

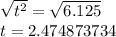
Rounding to the nearest tenth:

t=2.5 seconds

Answer: It will take approximately 2.5 seconds for the screwdiver to reach the ground.

7. What is the value of c so that -9 and 9 are both solutions of x^2+c=103?

x=-9 or x=9 are solutions. Replacing the values in the equation:

`\left \{ {{(-9)^(2)+c =103} \atop {(9)^(2)+c=103}} \right.`

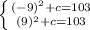
In both case we get:

`81+c=103`

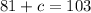
Solving for c: Subtracting 81 from both sides of the equation:

`81+c-81=103-81\\ c=22`

Answer: The value of c so that -9 and 9 are both solutions of x^2+c=103 is c=22