Question

Can you help me with my math questions

Answer 1

1. 15/8 and -15/8

2. Yes it is a perfect square.

3. a) 2.69 in

b) 6 in

c) 17.10 in

Explanation:

1. Find the factors of 64f² - 225

64f² - 225 = 0

(8f - 15)(8f +15) = 0

8f - 15 = 0 or 8f + 15 = 0

f = 15/8 or f = -15/8

2. Find whether it is a perfect square p² + 14p + 49

p² + 14p + 49 = 0

p² + 14p = -49

p² + 14p + 7² = -49 + 7²

(p + 7)² = 0

∴ p² + 14p + 49 = (p + 7)²

Yes it is a perfect square.

3 a)

36x² - 12x + 1 = 289

36x² - 12x = 288

x² - 1/3x + (1/6)² = 8 + 1/6

(x + 1/6)² = 49/6

x + 1/6 = ±2.8577

x = -3.02 and x = 2.69

3. b)

25x² - 50x + 25 = 1225

x² - 2x + 1 = 49

x² -2x + 1 =48 + 1

(x + 1)² = 49

x = ±√49 - 1

x = 6 and x = -8

3. c)

49x² - 56x + 16 = 289

49x² - 56x = 289 - 16

49x² - 56x = 273

x² - 1.1429x + 0.57² = 273 + 0.57²

(x - 0.57)² = 273.3265

x = ±√273.3265 + 0.57

x = 17.10 or x = -15.96

Answer 2

`p^2+2(7)p+7^2=(p+7)^2`

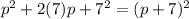
Justification:

Given:
`p^2+14p+49`

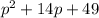
Split the middle term;

`=p^2+7p+7p+49`

Factor:

`=p(p+7)+7(p+7)`

`=(p+7)(p+7)`

`=(p+7)^2`

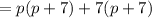
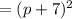
QUESTION 3a

The given expression for the area of the rectangle is
`36x^2-12x+1`.

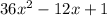This is equal to the indicated area which is
`289\;in^2`

This implies that

`36x^2-12x+1=289`

`\Rightarrow (6x-1)^2=289`

`\Rightarrow (6x-1)(6x-1)=289`

`\Rightarrow l=(6x-1),w=(6x-1)`

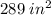
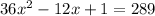
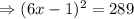
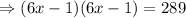
This implies that, the dimensions of the rectangle are equal;

Using the square root method, we obtain

`\Rightarrow (6x-1)=\pm √(289)`

`\Rightarrow (6x-1)=\pm 17`

`\Rightarrow 6x=1\pm 17`

`\Rightarrow 6x=18 \:or\:6x=-16`

`\Rightarrow x=3 \:or\:x=-(2)/(3)`

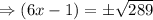
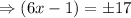
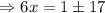
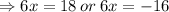
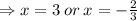
We discard the negative value.

The side length of this rectangle is

`\Rightarrow l=(6(3)-1)=17,w=6(3)-1=17`

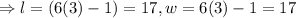
QUESTION 3b

The given expression for the area of the rectangle is
`25x^2-50x+25`.

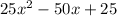This is equal to the indicated area which is
`1225\;in^2`

This implies that

`25x^2-50x+25=1225`

`25(x^2-2x+1)=1225`

`(5(x-1))^2=35^2`

`5(x-1)5(x-1)=49`

`\Rightarrow l=5(x-1),w=5(x-1)`

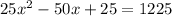
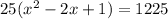
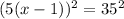
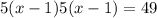
This implies that, the dimensions of the rectangle are equal;

Using the square root method, we obtain

`\Rightarrow 5(x-1)=\pm √(1225)`

`\Rightarrow 5(x-1)=\pm 35`

`\Rightarrow x=1\pm 7`

`\Rightarrow x=8 \:or\:x=-6`

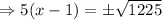
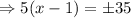
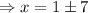
We discard the negative value.

The side length of this rectangle is

`\Rightarrow l=5(8-1)=35,w=5(8-1)=35`

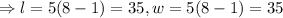
QUESTION 3c

The given expression for the area of the rectangle is
`49x^2-56x+16`.

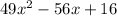This is equal to the indicated area which is
`289\;in^2`

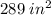
This implies that

`49x^2-56x+16=289`

`(7x-4)^2=289`

`(7x-4)(7x-4)=289`

`\Rightarrow l=(7x-4),w=(7x-4)`

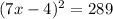
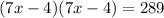
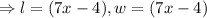
Applying the laws of indices gives;

`(7x-4)^2=17^2`

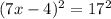
This implies that;

`7x-4=17`

`7x=21`

`x=3in.`

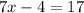
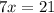
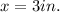
The side length of this rectangle is

`\Rightarrow l=7(3)-4=17\:in.,w=7(3)-4=17\:in.`

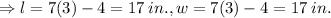
Dont forget that the square is also a rectangle.