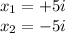Question

Can you help me with my work

Answer 1

number one is x=9,-9
number two is x=0
number three is x=12,-12
number four is 5i, -5i

Answer 2

For this case we have:

Question 1:

We want to know the solution of
`x ^ 2-81 = 0`

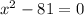
Adding 81 to both sides of the quadratic equation we have:

`x ^ 2-81 + 81 = 81\\x ^ 2 = 81`

Applying square root on both sides of the equation:

`\sqrt {x ^ 2} = \pm \sqrt {81}\\x = \pm 9`

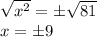
So, we have two solutions:

`x_ {1} = + 9\\x_ {2} = - 9`

Answer:

`x_ {1} = + 9\\x_ {2} = - 9`

Question 2:

In this case, we want to solve the following quadratic equation:

`2x ^ 2-26 = 0`

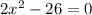
Adding 26 to both sides of the quadratic equation we have:

`2x ^ 2-26 + 26 = 26\\2x ^ 2 = 26`

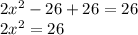
Dividing between 2 on both sides of the equation:

`\frac {2x ^ 2} {2} = \frac {26} {2}\\x ^ 2 = 13`

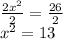
Applying square root on both sides of the equation:

`\sqrt {x ^ 2} = \pm \sqrt {13}`

`x = \pm \sqrt {13}`

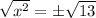
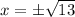
So, we have two solutions:

`x_ {1} = + \sqrt {13}\\x_ {2} = - \sqrt {13}`

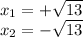
Answer:

`x_ {1} = + \sqrt {13}\\x_ {2} = - \sqrt {13}`

Question 3:

For this case, we have a quadratic function of the form
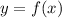`y = f (x)`, where
`f (x) = x ^ 2-144`. They ask us to find the roots. So:

`x ^ 2-144 = 0`

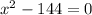
Adding 144 to both sides of the quadratic equation we have:

`x ^ 2-144 + 144 = 144\\x ^ 2 = 144`

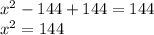
Applying square root on both sides of the equation:

`\sqrt {x ^ 2} = \pm \sqrt {144}\\x = \pm 12`

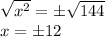
So, we have two solutions:

`x_ {1} = + 12\\x_ {2} = - 12`

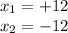
Answer:

`x_ {1} = + 12\\x_ {2} = - 12`

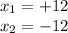
Question 4:

For this case we have a quadratic function of the form
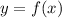`y = f (x)`, where
`f (x) = x ^ 2 + 25`

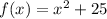
Antoine says he has no solution. We must verify:

`x ^ 2 + 25 = 0`

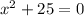
Subtracting 25 from both sides of the equation:

`x ^ 2 + 25-25 = -25\\x ^ 2 = -25`

Applying square root on both sides of the equation:

`\sqrt {x ^ 2} = \pm \sqrt {-25}`

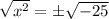
By definition:

`i = \sqrt {-1}\\i ^ 2 = -1`

So:

`x = \pm \sqrt {25i ^ 2}\\x = \pm5i`

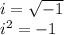
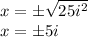
So, we have two solutions:

`x_ {1} = + 5i\\x_ {2} = - 5i`

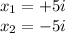
Answer:

`x_ {1} = + 5i\\x_ {2} = - 5i`