Answer:
Using formula:
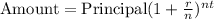
where
P is the principal
r is the annual rate in decimal
n is the number of compounding periods per year
t is the number of years.
As per the statement:
$3,500 after 2 years if it earns 1.5% compounded quarterly.
Here, P = $3500, t= 2 years, r = 1.5% = 0.015 and n = 4
then,
Substitute these values we have;
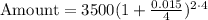
Or
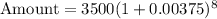
or
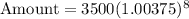
Simplify:
Amount = $3606.38852
Therefore, the value of an investment after 2 years is, $3,606.39