Question

Explain how you could write a quadratic function in factored form that would have a vertex with an x-coordinate of 3 and two distinct roots.

Answer 1

On edge, this would be the explanation. Just use these examples but change it up!

Answer 2

Answer: The answer is f(x) = (x-3)²-h = (x-3-√h)(x-3+√h).

Step-by-step explanation: We are given to write a quadratic function in factored form that would have a vertex with an x-coordinate of 3 and two distinct roots.

A quadratic function with vertex having x-coordinate k takes the form of a parabola as follows:

`f(x)+h=(x-k)^2.`

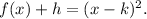
Here, 'k' and 'h' are both real.

Since we the the x-coordinate of the vertex as 3, so k = 3.

Therefore, the quadratic function becomes

`f(x)+h=(x-k)^2\\\\\Rightarrow f(x)=(x-k)^2-h\\\\\Rightarrow f(x)=(x-3-\sqrt h)(x-3+\sqrt h).`

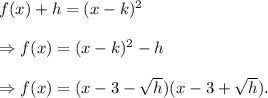
This is the required factored form of the quadratic function.

See the attached graph, where the x-coordinate of the vertex is 3 and h is taken to be 2 units.