On a piece of paper, graph f(x)=3•(2)^x

Question

asked Apr 25, 2020 119k views

2 Answers

Mandeep Kumar · Answer 1 · 2020-04-28T13:49:25+0000

The choice that matches the graph that is given to us is:

Graph D.

We know that a exponantial function is defined as:

f(x)=ab^x

If a>0

Then it is a exponential growth i.e. increasing if b>1

and is a exponential decay if: 0<b<1

Similarly if a<0

then it is a exponential decay or decreasing function if b>1

and it is a exponential growth or increasing function if 0<b<1

We are given a function f(x) as:

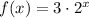
$f(x)=3\cdot 2^x$

We see that a=3>0 and b=2>1

Hence, the graph is a exponential growth i.e. the graph must be increasing for increasing values of x.

( Since both the graph are a graph of decreasing function)

then,
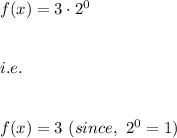
$f(x)=3\cdot 2^0\\\\\\i.e.\\\\\\f(x)=3\ (since,\ 2^0=1)$

Hence, we see that this condition is not satisfied in Graph C.

( Because at x=0 the graph passes through f(x)=1 i.e. the point (0,1) and not (0,3) )

Hence, graph C is also not the graph of this function.

So, we are left with graph D.

When we plot the graph of the function we see that it matches:

Graph D.