Question

Parallelogram RSTU is a rhombus. m∠R = 120°

What is m∠T

?

What is m∠RSU
?

Answer 1

see explanation

Explanation:

The opposite angles of a rhombus are congruent

∠T = ∠R = 120° ( opposite angles )

The triangle RSU is isosceles since the sides of the rhombus are congruent

Thus the base angles ∠RUS and ∠RSU are equal

The sum of the 3 angles in a triangle = 180°, hence

base angles = 180° - 120° = 60°

hence ∠RSU =
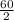`(60)/(2)` = 30°

Answer 2

1. 120°

2. 30°

Explanation:

Consider rhombus RSTU. In each rhombus two opposite angles are always congruent, then

m∠T=m∠R=120°.

The diagonals of the rhombus are rhombus's angles bisectors, then

`m\angle RSU=(1)/(2)m\angle S.`

The sum of two consecutive angles in a rhombus is always equal to 180°. Since m∠R = 120°, then

m∠S=180°-m∠R=180°-120°=60°

and

`m\angle RSU=(1)/(2)\cdot 60^(\circ)=30^(\circ).`