Question

Lisa is opening both a checking and savings account at her local bank. She deposits $50,000 into her checking account and $2,000 into her savings account. She will be withdrawing funds from her checking account over the course of each year to pay bills at an average rate of $2,500. Her savings account earns interest continuously at a rate of 5%.

If B represents the balance of the account and t represents the time in years since the account was opened, then which of the following systems of equations can be used to determine how long it will be before the balance in each account is equal?

Answer 1

D.
`\left\{\begin{matrix}B=50,000-2,500t \\B=2,000e^(0.05t) \end{matrix}\right.`

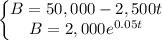
Explanation:

In checking account,

The initial amount = $50,000,

Lisa will be withdrawing funds from her checking account over the course of each year to pay bills at an average rate of $2,500.

Thus, the total amount she withdrawn in t years = 2500t,

Hence, the amount left in her checking account,

B = 50,000 - 2500t

Now, in saving account,

The principal amount = $ 2,000,

The rate of compounding continuously, r = 5% = 0.05,

Thus, the amount left after t years,

`B=Pe^(rt)`

`\implies B=2,000e^(0.05t)`

Hence, the systems of equations can be used to determine how long it will be before the balance in each account is equal,

`\left\{\begin{matrix}B=50,000-2,500t \\B=2,000e^(0.05t) \end{matrix}\right.`

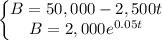
Option 'D' is correct.