Question

Ric made two investments: Investment \text{Q}Q has a value of \$500$500 at the end of the first year and increases by \$45$45 per year. Investment \text{R}R has a value of \$400$400 at the end of the first year and increases by 10\%10% per year. Eric checks the value of his investments once a year, at the end of the year. What is the first year in which Eric sees that investment \text{R}R's value exceeded investment \text{Q}Q's value?

Answer 1

Answer: 9 year (approx)

Explanation:

Since, In the Investment R,

The initial amount = $500

Which is increasing by $45 per year,

Thus, the total amount after x years in investment R = 500 + 45 x

In the investment Q,

The initial amount = $400

Which is increasing by 10% per year,

Thus, the total amount after x years in investment Q =
`400( 1 + (10)/(100))^x = 400(1+0.1)^x = 400(1.1)^x`

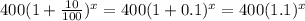
Since, the intersection point of the equations y =500+45x and y = 400(1.1)^x

are (-6.178, 221.992) and (8.069, 863.12)

But we can not take a negative number as a number of year,

Thus, the year in which both investment will equal is 8.069

After that the investment Q will be exceed the investment R,

⇒ The first year at which the investment Q will be exceed the investment R is approx 9th year.

Answer 2

10th year

Explanation:

Ric made two investments.

Investment Q

Amount = $500 at end of the year

Increase $45 per year.

Value of investment after x year

`A_(Q)=500+45(x-1)`

we take time (x-1) because investment was end of first year.

Investment R

Amount = $400 at end of the year

Increase 10% per year.

Value of investment after x year

`A_(R)=400(1+.1)^(x-1)`

we take time (x-1) because investment was end of first year.

Eric checks the value of his investments once a year, at the end of the year.

Eric sees that investment R's value exceeded investment Q's value

Investment R > Investment Q

`400(1+.1)^(x-1)>500+45(x-1)`

Using graphing calculator

`x>9.06`

Hence, In 10th year Investment R could be greater than Investment Q