Answer:
Explanation:
Alright, lets get started.
Please refer the diagram I have attached.
The point (8, -15) shows it is in 4th quadrant.
side X is 8 and side Y is -15.
We can find side R with help of Pythagorean theorem.
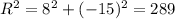
Taking square root,
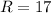
sinΘ=
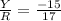
cosΘ=
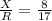
tanΘ=
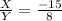
cscΘ=

secΘ=
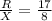
cotΘ=
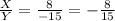
Answer
Hope it will help :)