Question

to estimate the height of the jin mao tower in shanghai , a tourist sights the top of the tower form a mirror that is 86.7 meters from the tower.The mirror is on the ground and faces up . The tourist is 0.4 meters from the mirror, and the distance from his eyes to the ground is 1.92 meters

Answer 1

The height of the tower = 420.48 meters

Explanation:

For better understanding of the solution, see the figure attached below :

Let the height of the tower be x meters

Now, using the laws of reflection : angle of reflection = angle of incidence

Also, both the tower and the tourist are standing parallel to each other

⇒ ∠A = ∠i ( Alternate interior angles are equal)

Similarly, ∠D = ∠r ( Alternate interior angles)

But, ∠i = ∠r

⇒ ∠A = ∠D

Also, the tourist and the tower is perpendicular to the ground surface.

⇒ m∠B = m∠E = 90°

Now, in ΔABC and ΔDEC

∠A = ∠D (Proved above)

m∠B = m∠E = 90°

So, by AA postulate of similarity of triangles, ΔABC ~ ΔDEC

As the sides of similar triangles are proportional to each other

`(AB)/(DE)=(BC)/(EC)\\\\\implies(1.92)/(x)=(0.4)/(87.6)\\\\\implies x=(87.6* 1.92)/(0.4)\\\\\bf\implies x = 420.48\textbf{ meters}`

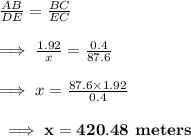
Hence, The height of the tower = 420.48 meters