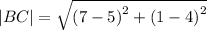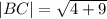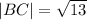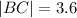QUESTION 1a.
The parallel sides of a trap-ezium form its bases.
We need to determine the slope of each side to find the sides that are parallel.
For side joining A (2, 4) and B (5, 4), the slope is
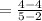
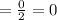
For the side joining, C (7, 1), and D (0, 1), the slope is,
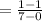
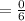
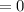
Recall that a trap-ezium has just one pair of sides parallel.
Hence the parallel sides are, AB and CD because their slopes are equal.
Therefore the bases are AB and CD.
QUESTION 1b.
We want to find the length of the line connecting A(2,4) and D(0,1).
This is given by the formula,
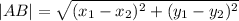
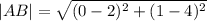
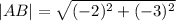

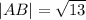

QUESTION 3
We want to find the length of the line connecting B(5,4) and C(7,1).
We use the distance formula again to obtain,