Question

Suppose a triangle has two sides of length 42 and 35 and that the angle between these two sides is 120. What is the length of thr third side of the triangle

Answer 1

66.78 units.

Explanation:

We have been given that a triangle has two sides of length 42 and 35 and that the angle between these two sides is 120. We are asked to find the length of third side of the triangle.

We will use law of cosines to find third side of triangle as:

`c^2=a^2+b^2-2ab\cdot\text{cos}(C)`

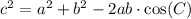
Upon substituting our given values, we will get:

`c^2=42^2+35^2-2\cdot42\cdot35\cdot\text{cos}(120^(\circ))`

`c^2=1764+1225-2940\cdot-0.5`

`c^2=1764+1225+1470`

`c^2=4459`

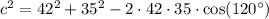
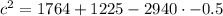
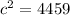
Take square root of both sides:

`√(c^2)=√(4459)`

`c=66.775744099`

`c\approx 66.78`

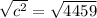
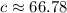
Therefore, the length of third side of our given triangle would be approximately 66.78 units.