Answer:
As per the statement:
You can see the diagram as shown below.
Distance of fireman stands away from the building = 30 m
Length of the ladder = 50 m
Using Cosine ratio:
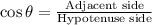 ....[1]
....[1]
From the diagram:
Adjacent side = 30 m
Hypotenuse side = 50 m
Substitute these values in [1] to solve for angle of elevation(
 )
)
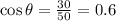
or
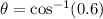
Simplify:
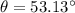
Therefore, the angle of elevation to the closest degree of the ladder is 51.13 degree