Question

From 2006 through 2016, suppose the number of dogs, D, and the number of cats, C, (in hundreds) adopted from animal shelters in a region of the U.S. are modeled by the equations D = 2n + 3 and C = n + 4, where n is the number of years since 2006.

a. Write a function that models the total number T of dogs and cats adopted in hundreds for this time period.
b. If this trend continues, how many dogs and cats will be adopted in 2020?

Answer 1

a.
`T=3n+7`

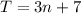
b. 4900.

Explanation:

We have been given that the number of dogs, D, and the number of cats, C, (in hundreds) adopted from animal shelters in a region of the U.S. are modeled by the equations
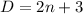`D=2n+3` and
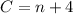`C=n+4`, where n is the number of years since 2006.

a. The total number T of dogs and cats adopted in hundreds for the time period 2006-2016 will be the sum of number of adopted dogs and cats.

`T=D+C`

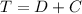
Upon substituting value of D and C is our above equation we will get,

`T=(2n+3)+(n+4)`

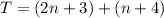
Upon removing parenthesis we will get,

`T=2n+3+n+4`

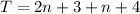
Let us combine like terms.

`T=(2n+n)+(3+4)`

`T=3n+7`

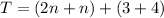
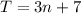
Therefore, the function
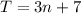`T=3n+7` models the total number, in hundreds, of dogs and cats adopted from 2006 to 2016.

b. To find the number of adopted dogs and cats in 2020, firstly, we will subtract 2006 from 2020 to find the value of n.

`n=2020-2006=14`

Let us substitute n=14 in our equation to get the number of dogs and cats adopted in 2020.

`T=3*14+7`

`T=42+7`

`T=49`

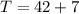
Since our function gives the number of dogs and cats in hundreds, so the number of dogs and cats adopted in 2020 will be:
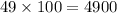`49* 100=4900`.